DeepSeek今日在Hugging Face上发布了一个名为DeepSeek-Prover-V2-671B的新模型。
该模型以 DeepSeekMath-Base 为基础,经针对数学定理证明任务进行了强化。
它不仅会解数学题,而且还能自动写出完整的数学证明过程。
DeepSeek-Prover-V1.5 是什么
DeepSeek-Prover-V1.5 是一个用人工智能来写数学证明的系统,它能根据一个数学命题,自动生成符合要求的数学证明,写成 Lean 4 语言。这种语言是数学家用来做“形式化证明”的标准工具。
换句话说,它是一个会“认真做数学题”的 AI 助手,特别擅长在电脑上严格地验证数学定理是否成立。
这个模型解决了什么问题?
在传统数学研究中:
- 定理的正确性验证高度依赖人工逻辑推理;
- 形式化证明虽能提高数学的严谨性,但手工编写效率低、门槛高;
- AI 模型虽然可以“生成答案”,但缺乏可验证的逻辑推导能力。
DeepSeek-Prover-V1.5 的目标是解决这些痛点:
构建一个能基于逻辑规则、语言建模、搜索策略,自动给出“可验证”数学证明过程的系统。
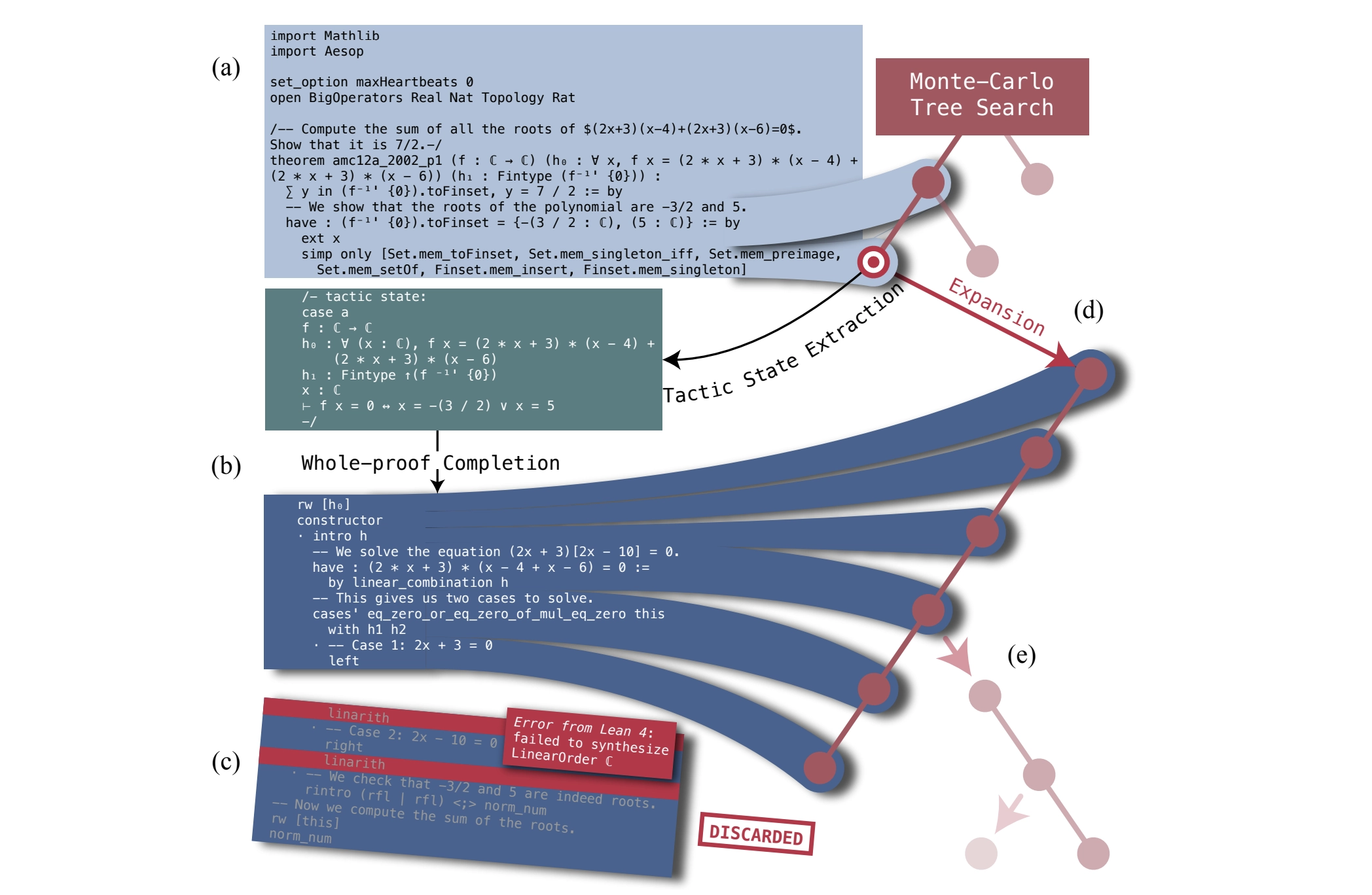
它有哪些主要功能和特点?
1. 🔍 专注于“形式化数学证明”
这个 AI 不只是算算数、做逻辑推理,而是能写出符合严格规范的、可以被计算机验证通过的完整证明过程。
2. 📚 支持 Lean 4 系统
Lean 是一个越来越受欢迎的数学证明工具,很多数学家和研究人员都在用它来做大规模的数学项目。DeepSeek-Prover-V1.5 能写出符合 Lean 4 标准的证明代码。
3. 🧩 支持两种证明方式
- 整体生成(Whole-proof):一次生成完整的证明过程,速度快,适合简单题。
- 逐步生成(Proof-step):一步步写,每一步都用 Lean 检查正确性,适合复杂题。
这个模型把这两种方式结合起来,变得更加灵活、实用。
🧠 模型是怎么训练出来的?
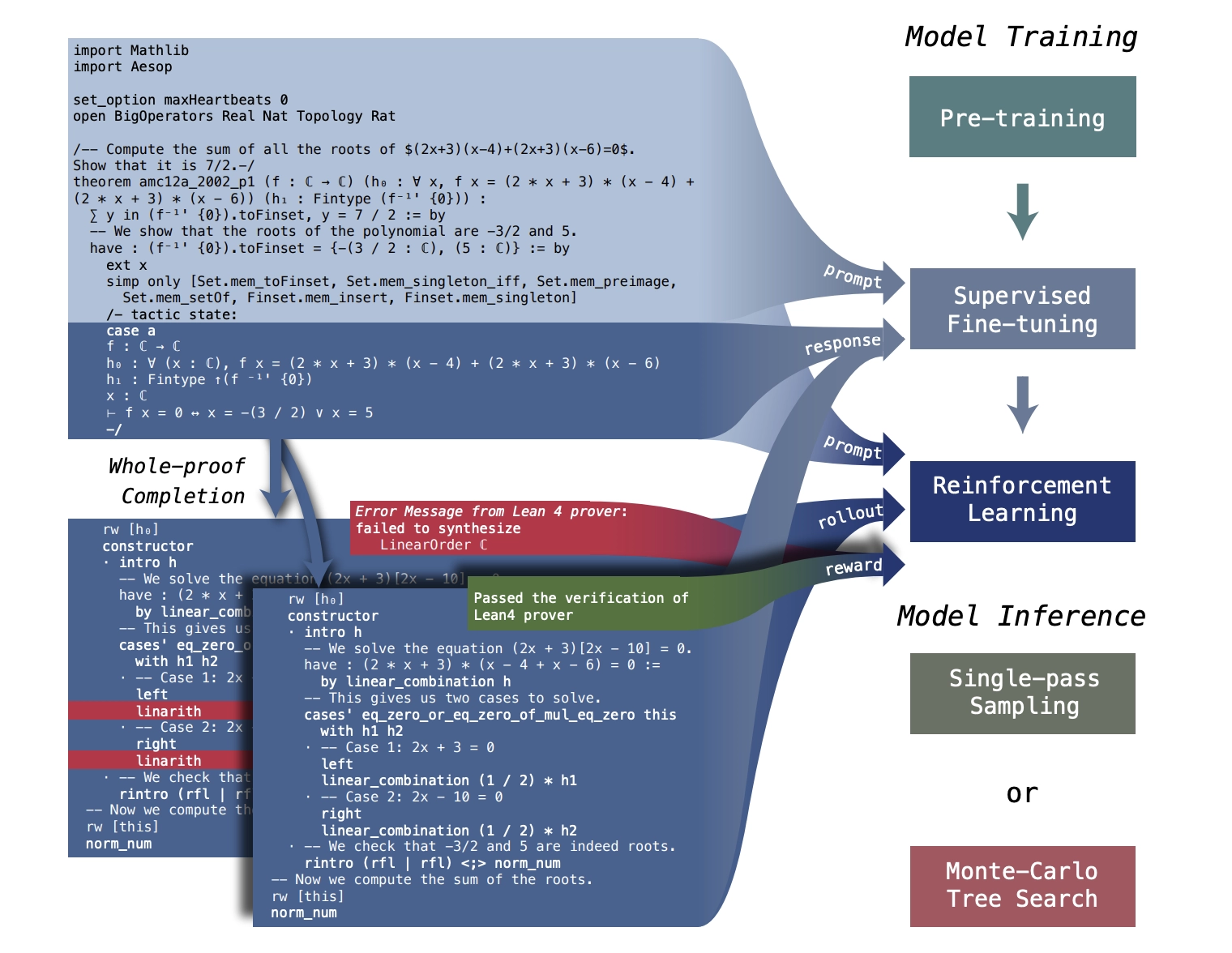
它的训练过程分为三大阶段,每个阶段都引入了更高层次的数学认知与推理能力。
📘 第一阶段:数学语言预训练(Pretraining)
使用自研的 DeepSeekMath 数据集进行预训练:
- 涵盖大量数学文本、公式、结构化定理描述;
- 目标是让模型熟悉 数学语言的表达方式与逻辑框架;
- 相当于给 AI 打下理解“数学语言”的基础语感。
🧑🏫 第二阶段:监督微调(Supervised Fine-Tuning, SFT)
在高质量的数学证明语料基础上,执行监督学习:
- 训练数据来源于 Lean 4 编写的真实定理与证明;
- 模型通过模仿学习,掌握了人类写作证明的通用逻辑模板;
- 能从命题出发,构造一套严密且语法正确的 Lean 4 证明步骤。
这一阶段重点在于:提升模型生成结构化证明的能力和准确性。
🎮 第三阶段:强化学习 + 搜索优化(RLPAF + RMaxTS)
这是 DeepSeek-Prover-V1.5 相比上一版本最核心的提升:
- RLPAF:使用证明反馈的强化学习
- RLPAF(Reinforcement Learning from Proof Assistant Feedback)通过引入 Lean 4 提供的反馈(如验证通过/失败)来对模型进行奖励惩罚;
- 类似于“做题打分”,模型从每次尝试中“学会什么样的写法是可行的”。
- RMaxTS:基于奖励驱动的蒙特卡洛树搜索
- 一种专为证明搜索定制的策略改进版本;
相比传统一次性生成全套证明,它可以:
- 在多路径中展开尝试;
- 评估中间步骤的“潜力”;
- 最终汇聚到最优路径;
- 显著提升了在复杂题目中的成功率与稳定性。
📊 性能指标:实际表现如何?
模型在两个权威数学形式化验证基准测试中表现优异:

miniF2F:注重逻辑基础与常见中学数学难题;
ProofNet:涵盖代数、离散数学、集合论等更高阶抽象命题。
在两个标准测试上,DeepSeek-Prover-V1.5 的准确率是目前开源模型中最好的:
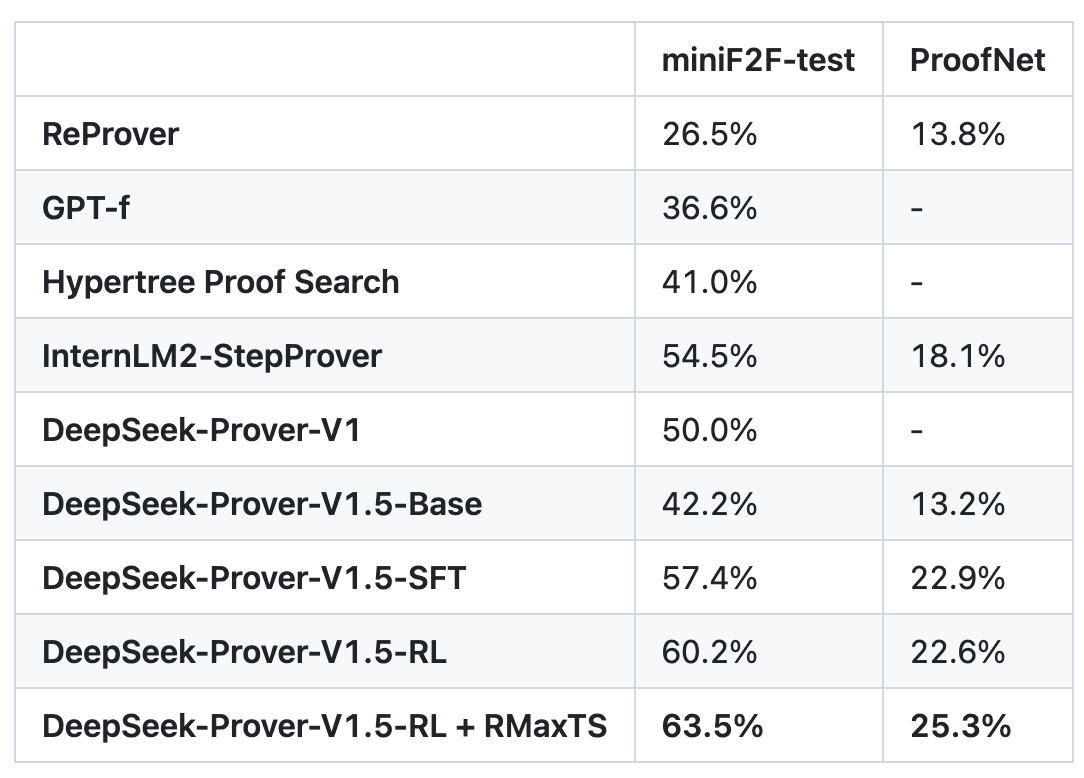
- 在高中数学题测试中,成功率从 50% 提高到了 63.5%。
- 在大学数学题测试中,成功率从 18.1% 提高到了 25.3%。
- 是目前最强的开源形式化数学证明 AI 系统之一。
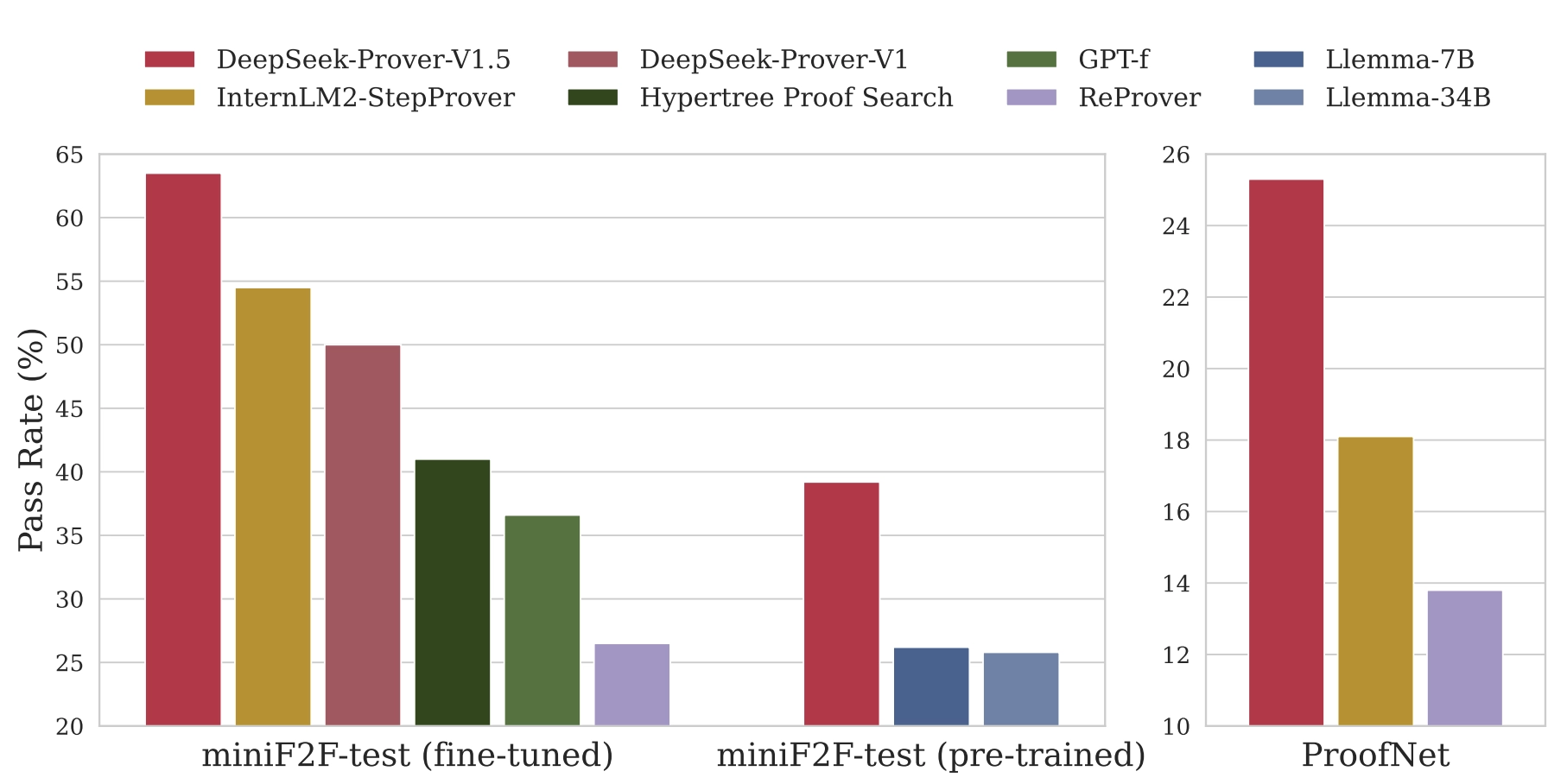
远超很多知名模型,比如 GPT-3.5、GPT-4 和其他数学证明 AI。
🛠️ 模型版本有哪些?

所有模型均已在 HuggingFace 上公开,可直接用于部署和微调。
GitHub:https://github.com/deepseek-ai/DeepSeek-Prover-V1.5
论文:https://arxiv.org/pdf/2408.08152
补充知识
🧾 什么是 Lean 4?
Lean 4 是一个专门用来做“形式化数学证明(Formal Proofs)”的编程语言和工具系统,由微软研究院开发。它既是一门编程语言,也是一个交互式定理证明器。
可以这样理解:
💡 Lean 4 = 数学 + 编程 + 自动检查对错的超级计算器
✍️ 传统写数学证明 vs 用 Lean 写数学证明
传统数学证明:
- 在纸上写:
“设三角形 ABC……由勾股定理得……” - 老师看得懂,但电脑完全不懂;
- 没法验证你写得对不对,也不能自动推理。
用 Lean 写的数学证明:
``` theorem my_thm : ∀ a b : ℕ, a + b = b + a := by simp
```
- 这是一段可以 被计算机执行和验证的数学逻辑;
- Lean 会自动检查这段推理是否严格正确;
- 没有模糊空间,必须完全逻辑严密;
- 如果错了,它会指出是哪一步有问题。
🏗️ Lean 4 的几个特点

🧑🏫 为什么 DeepSeek-Prover 专为 Lean 4 设计?
因为:
- Lean 4 是形式化数学界的“标准语言”之一,很多前沿数学项目都在用;
- 它支持 结构化表示定理与证明,非常适合 AI 模型理解和学习;
- 它本身支持“构造性逻辑”,便于编写可验证、可执行的证明程序;
- DeepSeek-Prover 就像一个“AI 学生”,学会用 Lean 4 写出完全正确、可执行的证明!
✅ 总结一句话:
Lean 4 是一个严谨的数学编程语言,让数学证明可以被计算机理解、验证与执行。DeepSeek-Prover 就是学会了用 Lean 4 写“正规数学论文”的 AI 数学家。